How To Calculate Damping Force
In a system, damping explains how apace the organisation will return to a state of rest after some external strength has acted upon information technology. For instance, in control systems, the goal is oft to stop a system from spinning or vibrating. The damping ratio expresses that response as a ratio between the bodily damping of the organization and the critical damping coefficient. Information technology is expressed as follows:
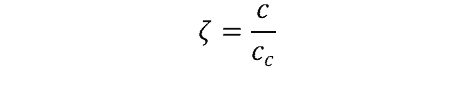
where:
- ζ is the damping ratio
- c is the actual damping coefficient
- cc is the critical damping coefficient
The value of ζ volition determine the kind of damping that is seen past the organisation, which volition enable an engineer to make necessary changes to the system to attain the desired end state.
The ideal damping state of the arrangement is referred to equally disquisitional damping. When a system is critically damped, the damping coefficient is equal to the critical damping coefficient and the damping ratio is equal to i.
Contents
- Critical Damping Explained
- Using the Critical Damping Coefficient
- Finding the actual damping coefficient
- From damping coefficient to damping ratio
- Critically damped arrangement
- Overdamped system
- Underdamped system
- Undamped organisation
- Applications of the Critical Damping Ratio
- Expanding Across One Dimension
- Fundamental Considerations
Critical Damping Explained
The critical damping coefficient is the solution to a second-order differential equation that is used to evaluate how quickly the system volition return to its original (unperturbed) state. For a unmarried degree of freedom arrangement, this equation is expressed equally:
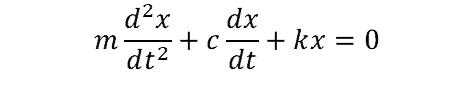
where:
- 1000 is the mass of the system
- c is the damping coefficient
- k is the leap rate
In the instance of critical damping, c volition be cc and can exist determined from the following:
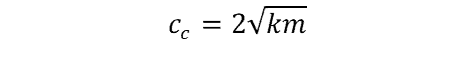
Because damping is only considered for harmonic (i.eastward., oscillating) systems, the equation for critical damping tin exist written equally follows:
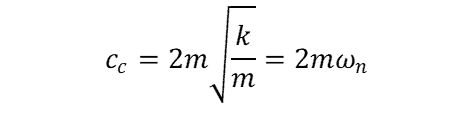
where ωn is the natural frequency of the system as it oscillates. The natural frequency of the system can be adamant in several ways, depending on the actual parameters of the system.
The disquisitional damping coefficient is the idealized coefficient for damping the organisation. The actual damping of a organization will be some value other than the critical damping coefficient, which is where the critical damping ratio comes into play.
Using the Critical Damping Coefficient
Using the disquisitional damping coefficient, it is possible to determine the critical damping ratio with the equation introduced above. The value of the critical damping ratio may exist a desired value, or it may be a calculated value.
If the value is established equally a desired value for an engineering awarding, the actual damping coefficient will be calculated. If the actual damping coefficient is known, then the critical damping ratio tin be calculated to notice how the system is operating.
Finding the actual damping coefficient
If the system has been modeled or can be tested in some way, it is possible to determine what the actual damping coefficient is. That value, c in the equation, is divided past the disquisitional damping coefficient, cc in the equation, to find the ratio.
In that location are a variety of ways to calculate the damping coefficient of a arrangement, most of which are specific to certain applications. However, they all come up down to solving the second-order differential equation. This tin be accomplished with numerical methods, analytical methods, or test methods.
From damping coefficient to damping ratio
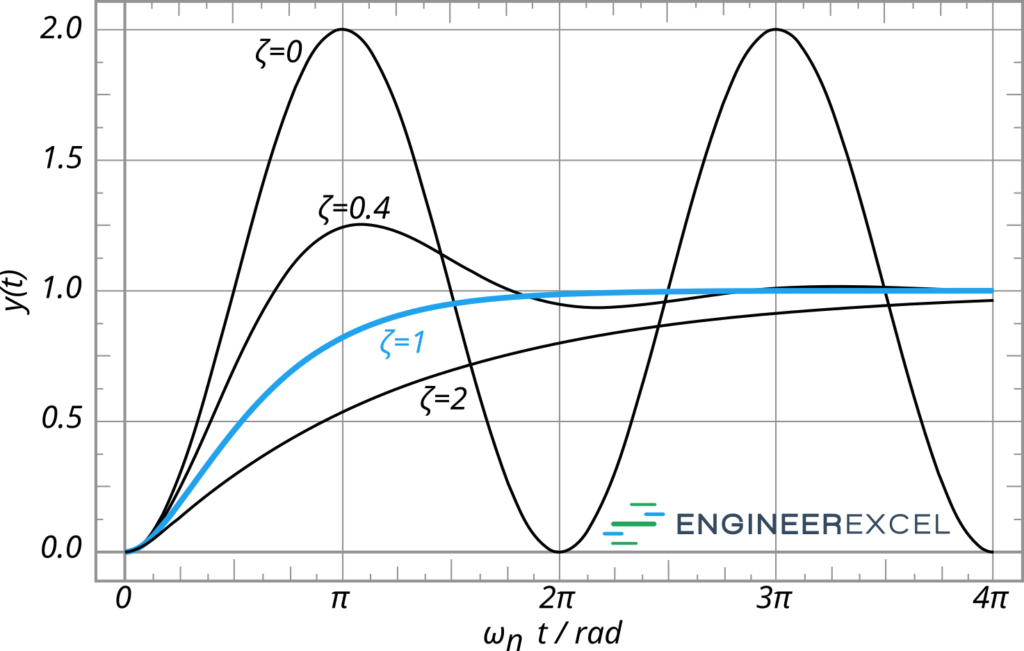
As can exist seen in the equation for the damping ratio, the actual damping coefficient is divided by the disquisitional damping coefficient. This means that the ratio will either be greater than or less than one. If the value of ζ is greater than one, the arrangement is said to be overdamped. If the value is less than one, the system is considered underdamped.
Critically damped organization
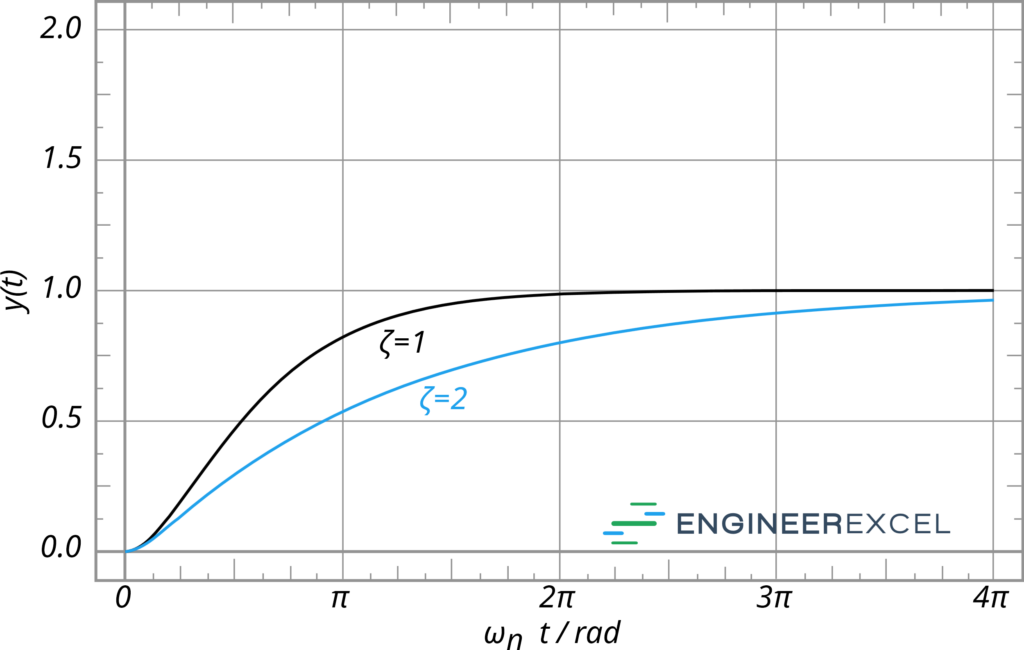
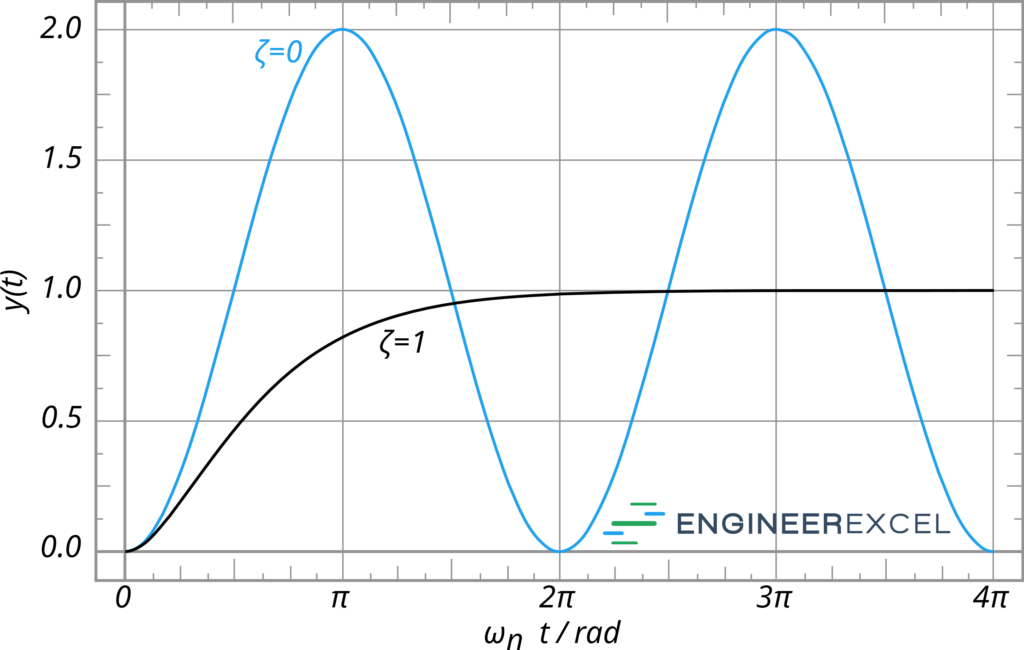
If the value of the damping ratio works out to exist exactly one (or as close to one as possible), then the system is said to be critically damped. This means that the actual damping coefficient is equal to (or very nearly equal to) the critical damping coefficient. In this case, the system will return to the ideal state more quickly than the overdamped system but will not overshoot that ideal state as the underdamped arrangement will do.
Overdamped organization
An overdamped system will return to its ideal state more slowly than the arcadian (i.e., critical) system. This may be desired, or it may bear witness to exist problematic. Overdamping a system means that at that place is more time to correct any problems, which can be benign for systems where overshooting is non a good consequence.
Underdamped system
An underdamped system will render to its ideal state more chop-chop than nether a critical system. The system will oscillate back and along, overshooting the ideal state in both the positive and negative direction, and the magnitude of that oscillation will diminish over fourth dimension until information technology is no more. This can be a adept thing if the goal is achieving a stable state quickly, but if the overshooting volition exist a problem, and then underdamping the system is not the way to become.

Undamped organisation
It is possible for a organisation to have no damping at all. This would exist a case where the damping ratio is equal to nil and means that the system will continue to oscillate forever, never reaching that ideal state. Undamped systems are generally non something that engineers aim for, although some applications do exist. However whatsoever system will have some damping due to the activeness of external forces.
Applications of the Disquisitional Damping Ratio
When solving engineering problems, understanding and applying damping to a system tin be very important. Considering the system in question can exist described using a second-order differential equation, information technology is possible to summate the critical damping coefficient relatively hands. This value tin then be used to calculate other parameters for the system.
Depending on the desired system outcome, underdamped, critically damped, or overdamped, the damping ratio tin be used to determine the platonic actual damping coefficient. With the calculated actual damping coefficient, the system tin can be designed in such a way equally to limited that coefficient.
For a system that is to be critically damped, the actual damping coefficient volition be set to the value of the critical damping coefficient. From that bespeak, the value of k in the system equation can be determined to consummate the organization design.
Past taking into consideration that it would exist near impossible to accept an actual damping coefficient that was exactly equal to the critical damping coefficient, some sort of tolerance can be applied such that the critical damping ratio was equal to some predetermined value very close to i. That ratio would then be applied to the critical damping coefficient, and that value c would be used in the second-order differential equation to solve for chiliad and the motion of the system.

Expanding Beyond Ane Dimension
Most real systems are going to take more than just a single dimension. In fact, most systems are going to have as many as vi degrees of freedom (DOF). This means that the equations of move will include ten-, y-, and z-directions likewise every bit rotations about each of those axes.
All the same, expanding the disquisitional damping ratio beyond a one-dimensional organization merely involves including the boosted dimensions in the differential equation. Moving from ane dimension to multiple dimensions will include some boosted calculations, but the primal concepts of solving for and using the damping coefficients volition remain the aforementioned.
Central Considerations
When using the critical damping ratio to evaluate the damping of a system, in that location are some things that demand to be taken into consideration.
The organisation that is being modeled needs to have some sort of harmonic move. For a control system, this could be simple harmonics (oscillations) about a single centrality, or up to a full 6 DOF system with oscillations and rotations nearly all three axes similar a flying simulator.

The critical damping coefficient is an expression of the idealized and describes the system equally it returns to the ideal state after a forcefulness has acted upon it. The ratio of the actual damping to this disquisitional damping is the critical damping ratio and can exist used to express whether the system is underdamped, critically damped, or overdamped (or, undamped).
Using the critical damping ratio, an engineer tin can decide other parameters of the arrangement to model either the desired behavior or the observed behavior. Modeling the desired behavior allows an engineer to change parameters to accomplish a desired outcome. Modeling the observed beliefs of a arrangement allows an engineer to make up one's mind a way to control the behavior of the system to achieve some desired finish state.
Because the critical damping ratio is one coefficient divided past another coefficient, there are no units associated with it.
How To Calculate Damping Force,
Source: https://engineerexcel.com/critical-damping-ratio/
Posted by: gravellecousine.blogspot.com


0 Response to "How To Calculate Damping Force"
Post a Comment